EXPLICATIONS
1. Principe
Séquencement
du plan
Le plan, une matrice 2D de pixels, est décomposé en séquences
carrées de quatre pixels mitoyens. Chaque pixel a une couleur et
il y a quatre couleurs possibles :
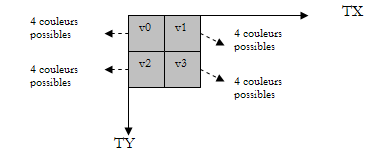
Les quatre couleurs sont les nombres 0,1,2,3 qui vont correspondrent aux
quatre premiers indices d’une palette 8 bits de 256 couleurs :
aaaaà l’indice 0 -> du noir
aaaaà
l’indice 1 -> du rouge
aaaaà
l’indice 2 -> du vert
aaaaà
l’indice 3 -> du bleu
Une séquence
de quatre pixels a ainsi 4couleurs*4couleurs*4couleurs*4couleurs configurations
possibles c'est-à-dire 4 puissance 4 configurations. Chaque configuration
est considérée comme un état et il y a 256 états.
A partir d’une
initialisation du plan au départ, l’objectif est d’organiser
localement la transition des états de chaque séquence de
quatre pixels vers une nouvelle configuration et de constater sur l’ensemble
du plan l’évolution générale.
Etablir des transitions
Pour chaque état possible d’une séquence de quatre
pixels va correspondre un nouvel état via une règle de transformation
qui produise une nouvelle configuration de la séquence. Par exemple
:


Autres transitions
possibles, une permutation au hasard des valeurs de cellules. Eventuellement
la duplication de l’état courant sans aucune permutation
peut aussi être utilisée dans un mélange des principes
de transformation.
Obtenir
une transformation
Pour éviter que l’automate ne se stabilise il est nécessaire
d’avoir simultanément une mixité des principes de
transition afin que toutes les séquences de 4 pixels n’obéissent
pas aux mêmes principes de transition.
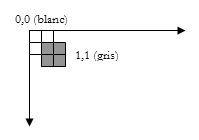
De plus le découpage
en séquences de quatre pixels fait l’objet d’une alternance.
Une fois sur deux est introduit un décalage de un pixel à
l’horizontal et à la vertical. C'est-à-dire que la
lecture du plan se fait de deux en deux pixels pour l’horizontal
comme pour la verticale, mais elle commence soit sur (0,0) et parcourt
le plan à partir des nombres pairs soit sur (1,1) et parcourt le
plan à partir des nombres impairs.
2. Mise en forme
et initialisation
Soit une résolution
d’écran définit par :
#define ECRAN_X 800
#define ECRAN_Y 600
Le plan est une matrice 2D
par exemple de dimensions :
#define TX ECRAN_X
#define TY ECRAN_Y/2
La surface sera simplement
une bitmap déclarée en globale, elle prendra la taille TX*TY
au moment de son allocation avec la fonction create_bitmap():
BITMAP*plan ;
Initialisation du plan
A l’initialisation chaque pixel prendra une valeur comprise entre
0 et 3 c'est-à-dire un nombre codé avec 2 bits (00 ou 01
ou 10 ou 11). La fonction d’initialisation attribue des valeur aux
pixels de la bitmap plan, par exemple une initialisation au hasard donne
une fonction du type :
aaaavoid init_rand()
aaaa{
aaaaint x,y ;
aaaaaaaafor (y=0 ; y<TY ; y++)
aaaaaaaaaaafor (x=0 ; x<TX ; x++)
aaaaaaaaaaaaaaplan->line[y][x]= (rand()%3)
? 0 : rand()%3+1;
aaaa}
Dans cet exemple, pour chaque position l’attribution
d’une valeur aléatoire entre 0 et 3 est pondérée
par un effet statistique afin de multiplier les 0.
D’autre possibilités d’initialisation
peuvent être mises en place notamment à base de formes, de
rectangles, des cercles, des triangles, voir des images, par exemple :
aaaavoid init_plan_rect()
aaaa{
aaaaint x,y,tx,ty,nb;
aaaaaaaafor
(nb=0; nb<TY+TX;nb++){
aaaaaaaaaaax=rand()%TX;
aaaaaaaaaaatx=rand()%(TX/4);
aaaaaaaaaaay=rand()%TY;
aaaaaaaaaaaty=rand()%(TY/4);
aaaaaaaaaaarectfill(plan,x,y,x+tx,y+ty,nb%4);
aaaaaaaa}
aaaa}
Codage des séquences
de quatre pixels
Comme une séquence est constituée de quatre pixels chaque
état est codé sur un octet de la façon suivante :
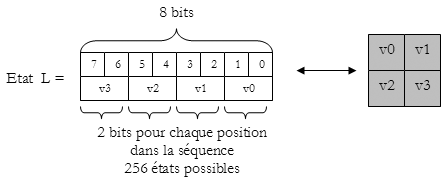
Pour chaque état,
la couleur de chaque position v0, v1, v2, v3 est accessible avec les opérateurs
bit à bit de la façon suivante :
aaaav0 = L & 3 ;
aaaav1 = (L >>2) & 3 ;
aaaav2 = (L >>4) & 3 ;
aaaav3 = (L >>6) & 3 ;
Codage des lois de transition
Les règles de transition
sont constituées d’un état « source »
et d’un état « résultant » après
transformation. Elles sont stockées dans une matrice de 256 * 4
entiers :
aaaaint lois[256][4] ;
Pour chaque état
de 0 à 255 est rangées aux indices 0,1,2,3 des colonnes
de la matrice une nouvelle configuration de couleurs pour les positions
v0, v1, v2, v3 d’une séquence de quatre pixels.
Exemples d’implémentations
d’une loi de transition à partir d’un état L
Rotation
à droite
Pour un état L = v3|v2|v1|v0 on veut L = v1|v3|v0|v2 (voir dessin
ci-dessus)
Cet exemple de transition peut être implémenté de
la façon suivante :
aaaavoid loi_permut_droite ( int L )
aaaa{
aaaaint v0,v1,v2,v3;
aaaaaaaa//
récupération de l'état pour L
aaaaaaaav0=
L & 3;
aaaaaaaav1=(L>>2)&3;
aaaaaaaav2=(L>>4)&3;
aaaaaaaav3=(L>>6)&3;
aaaaaaaa// correspondance,
nouvel état à partir de l'état L
aaaaaaaalois[
L ][0]=v2;
aaaaaaaalois[
L ][1]=v0;
aaaaaaaalois[
L ][2]=v3;
aaaaaaaalois[
L ][3]=v1;
aaaa}
Rotation
gauche
P pour un état L = v3|v2|v1|v0 on veut L = v2|v0|v3|v1
Cet exemple de transition peut être implémenté de
la façon suivante :
aaaavoid loi_permut_gauche ( int L )
aaaa{
aaaaint v0,v1,v2,v3;
aaaa// récupération de l’état
L
aaaaaaaav0=L&3;
aaaaaaaav1=(L>>2)&3;
aaaaaaaav2=(L>>4)&3;
aaaaaaaav3=(L>>6)&3;
aaaaaaaa// correspondance,
nouvel état à partir de l'état l
aaaaaaaalois[L][0]=v1;
aaaaaaaalois[L][1]=v3;
aaaaaaaalois[L][2]=v0;
aaaaaaaalois[L][3]=v2;
aaaa}
Permutations
aléatoires
P our un état L = v3|v2|v1|v0 on veut une permutation aléatoire
de v3, v2, v1 ou v0
Cet exemple de transition peut être implémenté de
la façon suivante :
aaaavoid loi_permut_rand ( int L )
aaaa{
aaaaint r1,r2,i,tmp,v[4];
aaaaaaaa//
récupération de l'état pour L dans un tableau
aaaaaaaav[0]=L&3;
aaaaaaaav[1]=(L>>2)&3;
aaaaaaaav[2]=(L>>4)&3;
aaaaaaaav[3]=(L>>6)&3;
aaaaaaaa// tirage
aléatoire de deux indices différents
aaaaaaaafor
(i=0; i<16;i++){
aaaaaaaaaaar1=rand()%4;
// au hasard un indice r1
aaaaaaaaaaawhile(
(r2=rand()%4)==r1){} // au hasard un second r2 différent du premier
aaaaaaaaaaatmp=v[r1];
// permutation des deux indices r1 et r2
aaaaaaaaaaav[r1]=v[r2];
aaaaaaaaaaav[r2]=tmp;
aaaaaaaa}
aaaaaaaa// correspondance,
nouvel état à partir de l'état L
aaaaaaaalois[
L ][0]=v[0];
aaaaaaaalois[
L ][1]=v[1];
aaaaaaaalois[
L ][2]=v[2];
aaaaaaaalois[
L ][3]=v[3];
aaaa}
Eventuellement,
si pas de permutation
Pour un état
L = v3|v2|v1|v0 on veut L = v3|v2|v1|v0
Cet exemple de transition peut être implémenté de
la façon suivante :
aaaavoid loi_duplique(int l)
aaaa{
aaaaint v0,v1,v2,v3;
aaaaaaaav0=l&3;
aaaaaaaav1=(l>>2)&3;
aaaaaaaav2=(l>>4)&3;
aaaaaaaav3=(l>>6)&3;
aaaaaaaalois[l][0]=v0;
aaaaaaaalois[l][1]=v1;
aaaaaaaalois[l][2]=v2;
aaaaaaaalois[l][3]=v3;
aaaa}
Réalisation d’un
ensemble transitionnel pour les 256 états possibles
Pour un état
possible nous disposons de plusieurs modèles correspondance, rotations
droite, gauche, permutations aléatoires, duplication de l’état.
Mais nous avons besoin d’un ensemble de 256 transitions, une pour
chaque état. De plus cet ensemble ne doit pas appartenir à
un modèle unique de transitions faute de quoi l’automate
se paralyse. Sauf dans le cas des transitions fondées sur des permutations
aléatoires, il est nécessaire de déstabiliser l’automate
par une mixité de principes des transitions. Un grand nombre de
possibilités peuvent être testées qui donnent des
résultats différents pour l’automate.
Ensemble
transitionnel aléatoire
Le plus simple est probablement un ensemble transitionnel aléatoire.
Il peut facilement s’implémenter de la façon suivante
:
aaaavoid ensemble_lois_rand()
aaaa{
aaaaint L;
aaaaaaaafor
(L=0; L<256; L++)
aaaaaaaaaaaloi_permut_rand(L);
aaaa}
Ensemble
transitionnel de lois avec des types mélangés
aaaavoid ensemble_lois_melange()
aaaa{
aaaaint L;
aaaaaaaafor
(L=0; L<256; L++)
aaaaaaaaaaaif
(rand()%3){
aaaaaaaaaaaaaaif
(rand()%2)
aaaaaaaaaaaaaaaaaloi_permut_droite(L);
aaaaaaaaaaaaaaelse
aaaaaaaaaaaaaaaaaloi_permut_gauche(L);
aaaaaaaaaaa}
aaaaaaaaaaaelse
aaaaaaaaaaaaaaloi_duplique(L);
}
3. Processus générateur
Lecture séquentielle
du plan
A partir d’un état
L l’utilisation des opérateurs bits à bits permet
de récupérer les valeurs de chacun des pixels de la séquence.
Dans l’autre sens à partir des pixels on peut reconstituer
un état de la façon suivante :
aaaaL= ( getpixel ( plan, x, y)aaaaaa
| aaaa// v0
aaaaaaaagetpixel
( plan, x+1, y) <<2 |aaaa // v1
aaaaaaaagetpixel
( plan, x, y+1) <<4 | aaaa// v2
aaaaaaaagetpixel
( plan, x+1, y+1) <<6 ) ; // v3
Ecriture dans le plan
Après lecture d’une
séquence dans le plan et déduction de l’état
L correspondant via l’utilisation de getpixel() et des opérateurs
bits à bits, l’écriture dans le plan du nouvel état
se fera tout simplement pour chaque pixel avec la fonction putpixel()
de la façon suivante :
aaaaputpixel (plan, x , y , lois[ L ][0]
) ;
aaaaputpixel (plan, x+1, y , lois[ L ][1]
) ;
aaaaputpixel (plan, x , y+1, lois[ L ][2]
) ;
aaaaputpixel (plan, x+1, y+1, lois[ L ][3]
) ;
Mise à jour
du plan
Le plan est parcouru par groupe
de quatre pixels, soit de 2 en 2 pour l’horizontale et la verticale.
De plus il est parcouru alternativement à partir des positions
paires puis des positions impaires.
aaaavoid update_plan(int decx,int decy)
aaaa{
aaaaint x,y,xp,yp,l ;
aaaaaaaafor
(y=decy; y<TY; y+=2)
aaaaaaaaaaafor
(x=decx; x<TX; x+=2){
aaaaaaaaaaaxp=
(x+1<TX)? x+1 : 0 ; // écran circulaire
aaaaaaaaaaayp=
(y+1<TY)? y+1 : 0 ;
aaaaaaaaaaa//
récupération de l'état d'un carré de 4 pixels
adjacents
aaaaaaaaaaal=aa
( _getpixel(plan,x,y)aaaaa |
aaaaaaaaaaaaaaa(_getpixel(plan,xp,y)<<2)
|
aaaaaaaaaaaaaaa(_getpixel(plan,x,yp)<<4)
|
aaaaaaaaaaaaaaa(_getpixel(plan,xp,yp)<<6)
);
aaaaaaaaaaa//
nouvelles valeurs avec table de correspondance,
aaaaaaaaaaa_putpixel(plan,x,y,lois[
l ][0]);
aaaaaaaaaaa_putpixel(plan,xp,y,lois[
l ][1]);
aaaaaaaaaaa_putpixel(plan,x,yp,lois[
l ][2]);
aaaaaaaaaaa_putpixel(plan,xp,yp,lois[
l ][3]);
aaaaaaaa}
aaaa}
|